Realizzazione siti internet
Siti web vetrina - Dinamici (CMS) su piattaforma wordpress ed e-commerce, dedicato alla vendita online.

Vanityweb non è solo una web agency ma un agenzia creativa con idee nuove ed originali con l'obiettivo principale di far crescere la vostra attività.
Sono numerosi gli strumenti che possiamo offrire nel campo della comunicazione online e tradizionale. Chiedici una consulenza, saremo contenti di aiutarti.
Per noi è importante che Il Cliente abbia le idee chiare sul servizio che offriamo a prescindere dal fatto che lo acquisti o no!
Realizziamo siti web per piccole, medie e grandi attività; siti vetrina (di presentazione), siti aziendali basati sul sistema di gestione autonoma dei contenuti (CMS) e siti dedicati alla vendita online di prodotti e/o servizi (E-commerce).
Posizionamento sui più importanti motori di ricerca (Google - Bing - Yahoo) per raggiungere le prime pagine grazie all'ottimizzazione naturale/organica dei contenuti e della struttura del sito.
Particolare attenzione ai servizi di annunci a pagamento per velocizzare ed incrementare la presenza online del vostro brand, di un prodotto, di un servizio.
Inoltre ci occupiamo di Social Media Marketing - generiamo visibilità sulle più importanti piattaforme gestendo le pagine di Facebook, Instagram, Twitter, Linkedin, Pinterest, Foursquare...

Siti web vetrina - Dinamici (CMS) su piattaforma wordpress ed e-commerce, dedicato alla vendita online.

Ottimizzazione siti per il miglior posizionamento sui più importanti motori di ricerca (Google - Bing)

Creazione campagne marketing con annunci a pagamento per essere subito in prima pagina

Gestione, personalizzazione e ottimizzazione pagine sociali (Facebook - Instagram - Pinterest - Twitter).
Siamo i tuoi Fotografi Certificati - Google Street View.
Assumici e realizzeremo per te, in pochissimo tempo,
il tuo FANTASTICO Virtual Tour a 360° di Alta Qualità!!!
AUMENTA LA VISIBILITÀ DELLA TUA AZIENDA/ATTIVITÀ SU GOOGLE.
Proponiamo servizi di grafica pubblicitaria professionale. Progetti grafici personalizzati. L'identità della tua attività è tutto! Fatti riconoscere.

Realizzazioni loghi aziendali vettoriali in Alta Risoluzione. Pratiche di registrazione del marchio nazionale, comunitario ed internazionale.

Progettazione e realizzazione grafica, dal biglietto da visita alla carta intestata e packaging. Personalizzazione gadget (penne- t-shirt - usb)

Realizzazioni grafiche digitali di impatto da utilizzare su canali digitali (siti - social - advertising) e supporti stampati (cartolloni - depliant - brochure etc..)

Servizi fotografici professionali in studio o in esterna. Still Life campionatura prodotti ed abbigliamento - Riprese fotografiche panoramiche con Drone.
Stampa materiale pubblicitario su qualsiasi tipo di supporto dal formato più piccolo (BDV, Brochure - Volantini, Carta intestata) a quello più grande, per spazi pubblicitari come manifesti 6x3 - Striscioni pvc - Insegne - Pannelli luminosi...
Pre e post produzione di video aziendali - Spot pubblicitari -
Riprese Aeree con Drone - Animazioni Cartoon
Novità, curiosità dal nostro blog. Rimani aggioranto!
Google Maps si aggiorna: ora ti dice dove ordinare il cibo con consegna a domicilio o da asporto.
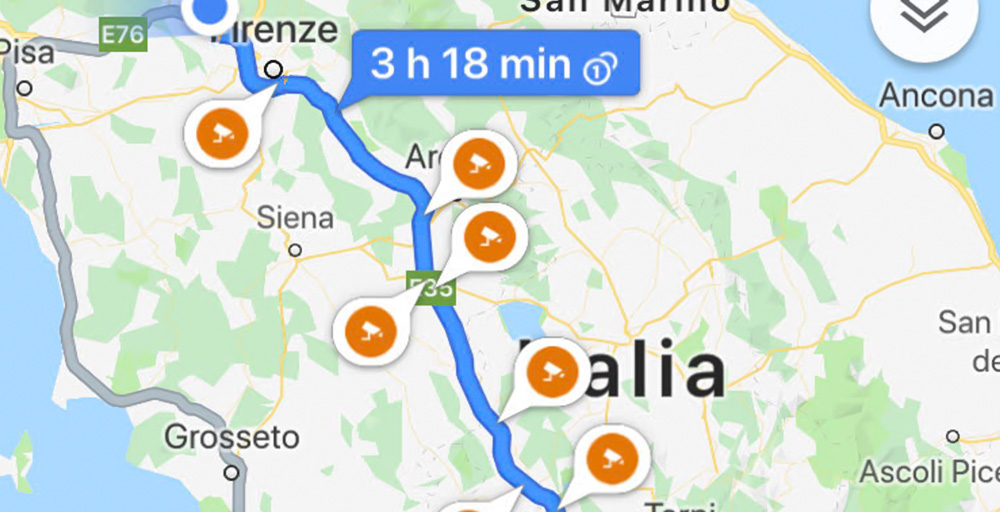
Finalmente Google Maps permette la segnalazione degli autovelox in oltre 40 Paesi, tra cui l’Italia.
Potrai navigare su Google Maps in tempo reale e trovare oggetti virtuali sullo schermo che potrebbero interagire con te in modo divertente, darti informazioni utili etc..

Quello che pensano di noi i nostri clienti è importante perché ci aiuta a migliorare!
Vanityweb di Luca Montecalvo
Via A. Toscanini, 22
59013 Montemurlo - PRATO
Siamo operativi in tutta la Toscana ed in particolare nelle province di Prato, Firenze e Pistoia.
Potete contattarci gratuitamente per ricevere informazioni, fissare un appuntamento o per avere un primo preventivo, sia da telefono fisso che da cellulare, chiamando il:
NUMERO VERDE GRATUITO 800 592776